
1 ) )// S in c e d s c r ( ) r e t u r n s a s t a t e space model SimpleSysDiscr = s s 2 t f ( d s c r ( SimpleSys, 0. Then compare this with the step response of the statespace representation (remember to set the initial state (x0) andstep size (u) correctly. Try this: obtain the step response of the converted transferfunction. T = u = 0.5* ones (1, l e n g t h ( t ) ) = cs im (u, t, SSsys ) Įvans ( SSsys ) //zoom i n// Conve r s i on from s t a t e space to t r a n s f e r f u n c t i o n :s s 2 t f ( SSsys )r o o t s ( denom( ans ) )spec ( A ) SSsys = s y s l i n ( c, A, B, C, D, x0 )

U = ones (1, 50) y = f l t s (u, DTSystem ) p l o t ( y ) // C lo s e t h i s when doneĪ = B = C = D = Z = %za = 0.1DTSystem = s y s l i n ( d, a*z /( z (1a ) ) ) Y7 = csim ( s t e p, t, CriticallyDampedSystem ) p l o t (t, y7 ) M = s2+6*s+9CriticallyDampedSystem = s y s l i n ( c, 9/m )r o o t s ( m )
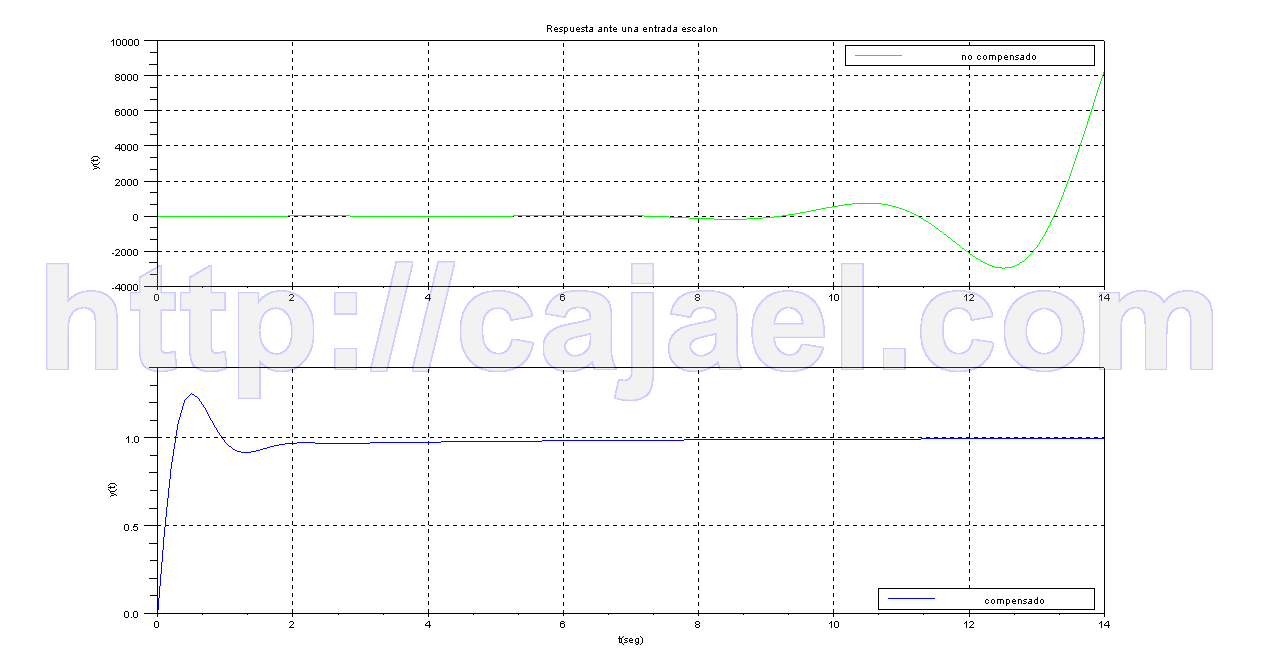
Y6 = csim ( s t e p, t, UndampedSystem ) p l o t (t, y6 ) R = s2+9UndampedSystem = s y s l i n ( c, 9/r )r o o t s ( r ) Y5 = csim ( s t e p, t, UnderdampedSystem ) p l o t (t, y5 ) Q=s2+2*s+9UnderdampedSystem = s y s l i n ( c, 9/q )r o o t s ( q ) Y4 = csim ( s t e p, t, OverdampedSystem ) p l o t (t, y4 ) P=s2+9*s+9OverdampedSystem= s y s l i n ( c, 9/p ) U3=s i n (5* t ) 圓 = csim ( u3, t, SimpleSys ) // s i n e r e s pon s e at d i f f e r e n tįMin=0.01, fMax=10bode ( SimpleSys, fMin, fMax ) U2=s i n ( t ) y2 = csim ( u2, t, SimpleSys ) // s i n e r e s pon s ep l o t (t, ) 0 1 : 1 5 y1 = csim ( s t e p, t, SimpleSys ) // s t ep r e s pon s ep l o t (t, y1 ) Po l y (0, s )K = 1, T = 1 // Gain and t ime con s t an tSimpleSys = s y s l i n ( c, K/(1+T*s ) )Īditya Sengupta, EE, IITB CACSD with Scilab De f i n i n g a f i r s t o r d e r system :s = %s // The qu i c k e r a l t e r n a t i v e to u s i n g s =


 0 kommentar(er)
0 kommentar(er)
